NCERT Solutions for Coordinate Geometry Class 10 Chapter 7 Ex 7.2 Maths has all the solutions to the questions provided in the NCERT Book of the latest edition.
Students are advised to practice all the questions to get good marks in the board examination.
| Textbook | NCERT |
| Class | 10 |
| Subject | Mathematics |
| Chapter | 7 |
| Exercise | 7.2 |
| Chapter Name | Coordinate Geometry |
Class 10 Maths Chapter 7 Exercise 7.2 Coordinate Geometry NCERT Solution
Find the coordinates of the point which divides the join of (–1, 7) and (4, –3) in the ratio 2 : 3.
Answer
Using section formula, when externally cut $$m=2$$, $$n=3$$
$$x=\frac{mx_{2}+nx_{1}}{m+n}$$ , $$y=\frac{my_{2}+ny_{1}}{m+n}$$
$$x=\frac{(2\times4)-(3\times1)}{2+3}=\frac{5}{5}=1$$
$$y=\frac{(2\times-3)+(3\times7)}{2+3}=\frac{-6+21}{5}=\frac{15}{5}=3$$
Points is (x,y) = (1,3)
Find the coordinates of the points of trisection of the line segment joining (4, –1) and (–2, –3).
Answer
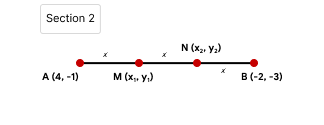
Trisect means
AM = MN = NB
Let it be ‘x’
AM = MN = NB = x
$$\frac{AM}{MB}=\frac{x}{2x}=1:2$$ (cuts internally)
$$\therefore$$ m:n = 1:2
$$x_{1}=\frac{(1\times-2)+2\times4}{1+2}=\frac{-2+8}{3}=2$$
$$y_{1}=\frac{(1\times-3)+2\times-1}{1+2}=\frac{-3-2}{3}=\frac{-5}{3}$$
$$m=(x_{1},y_{1})=\left(2, \frac{-5}{3}\right)$$
Now,
$$\frac{AN}{NB}=\frac{2x}{x}=2:1$$
$$\therefore m:n = 2:1$$
$$x_{2}=\frac{(2\times-2)+1\times4}{2+1}=\frac{-4+4}{3}=0$$
$$y_{2}=\frac{(2\times-3)+1\times-1}{2+1}=\frac{-6-1}{3}=\frac{-7}{3}$$
$$m=(x_{2},y_{2})=\left(0, \frac{-7}{3}\right)$$
To conduct Sports Day activities, in your rectangular shaped school ground ABCD, lines have been drawn with chalk powder at a distance of 1m each. 100 flower pots have been placed at a distance of 1m from each other along AD, as shown in Fig. 7.12. Niharika runs $$\frac{1}{4}$$th the distance AD on the 2nd line and posts a green flag. Preet runs $$\frac{1}{5}$$th the distance AD on the eighth line and posts a red flag. What is the distance between both the flags? If Rashmi has to post a blue flag exactly halfway between the line segment joining the two flags, where should she post her flag?
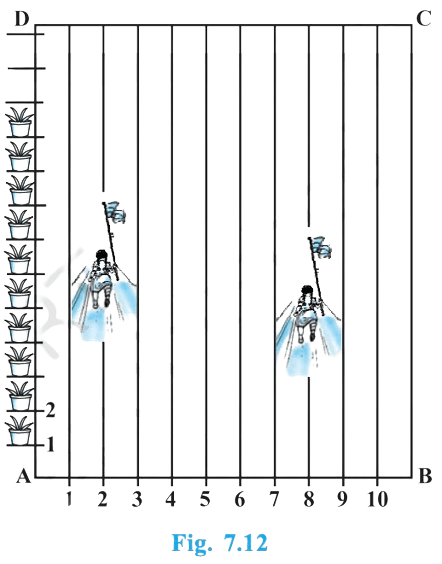
Answer
Niharika at Points $$\left(2,\frac{100}{4}\right)$$
⇒ (2, 25)
Preet at points = $$\left(8,\frac{100}{5}\right)$$
⇒ (8, 20)
Distance b/w Ninarika and Preet =
D = $$\sqrt{(8-2)^{2}+(25-20)^{2}}$$
⇒ $$\sqrt{(6)^{2}+(5)^{2}} = \sqrt{61}m$$
Rashmi at the midpoint of the line joining (2, 25) and (8, 20)
So ratio is (1:1)
m:n = 1:1
Let point of Rashmi (x,y)
$$x={1\times2+8\times1}{2}=5m$$
$$x={1\times20+1\times25}{2}=\frac{45}{2}m$$
Rashmi is on $$5^{th}$$ line and at a distance of $$\frac{45}{2}$$m
Find the ratio in which the line segment joining the points (– 3, 10) and (6, – 8) is divided by (– 1, 6).
Answer
Let the point (-1,6) cuts the line segment in the ratio of (K:1)
A = (-3, 10), B = (6, -8)
So,
$$-1=\frac{k\times6-3\times1}{k+1}$$
$$-k-1=6k-3$$
$$-1+3=6k+k$$
$$k=\frac{2}{7}$$
K : 1 = $$\frac{2}{7}:1$$ = 2 : 7
Find the ratio in which the line segment joining A(1, – 5) and B(– 4, 5) is divided by the x-axis. Also find the coordinates of the point of division.
Answer
Let x-axis cuts line segment in ration (K:1)
Point on x-axis (x,0)
A = (1,-5), B = (-4,5)
$$x=\frac{k\times-4+1\times1}{k+1}$$
$$0=\frac{k\times5+1\times-5}{k+1}$$
5k – 5 = 0
5k = 5
k = 1
So, the ratio is (1:1)
If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.
Answer
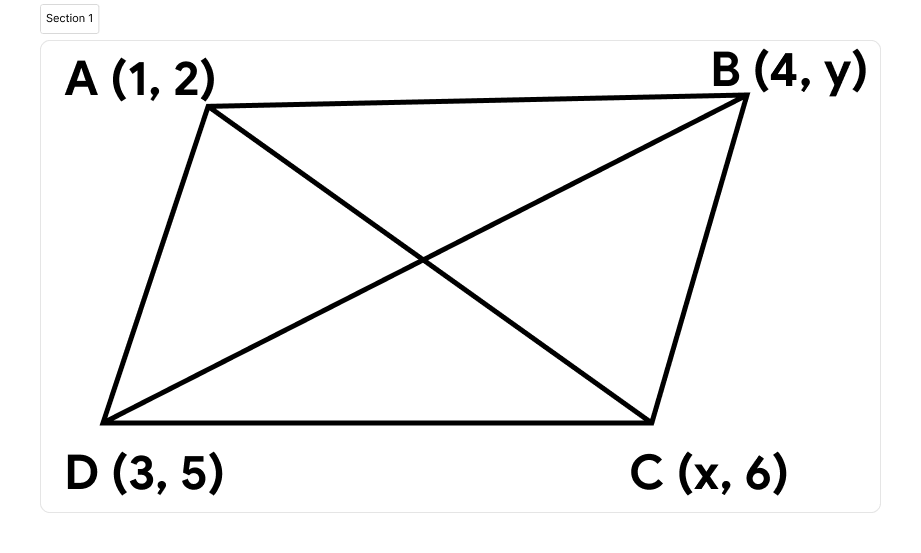
midpoint of AC = $$\left(\frac{x+1}{2},\frac{6+2}{2}\right)$$
midpoint of AD = $$\left(\frac{4+3}{2},\frac{y+5}{2}\right)$$
$$\frac{x+1}{2}=\frac{4+3}{2}$$
$$ x+1=7$$
$$x=6$$
Now
$$\frac{6+2}{2}=\frac{y+5}{2}$$
$$ 8=y+5$$
$$y=3$$
Find the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, – 3) and B is (1, 4).
Answer
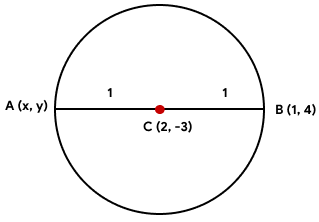
Centre divides diameter in equal
So,
m : n = 1 : 1
$$2=\frac{1\times1+1\times x}{2}$$
$$\frac{x+1}{2}=2$$
$$x=4-1= 3$$
Now,
$$-3=\frac{1\times4+1\times y}{2}$$
$$-6=4+y$$
$$y=-10$$
Point A = (3, -10)
If A and B are (– 2, – 2) and (2, – 4), respectively, find the coordinates of P such that AP = $$\frac{3}{7}$$AB and P lies on the line segment AB.
Answer
$$AP=\frac{3}{7}AB$$ —-(i)
AP + PB = AB —-(ii)
Put eq(ii) in eq(i)
$$AP=\frac{3}{7}(AP+PB)$$
7AP = 3 AP + 3 PB
4 AP = 3 PB
$$\frac{AP}{PB}=\frac{3}{4}=\frac{m}{n}=3:4$$
$$x=\frac{3\times2+4\times -2}{3+4}=\frac{6-8}{7}=\frac{-2}{7}$$
$$y=\frac{3\times-4+4\times -2}{3+4}=\frac{-12-8}{7}=\frac{-20}{7}$$
So point P = $$\left(\frac{-2}{7},\frac{-20}{7}\right)$$
Find the coordinates of the points which divide the line segment joining A(– 2, 2) and B(2, 8) into four equal parts.
Answer
$$\frac{PA}{PB}=\frac{}{}=1:3$$
$$x_{1}=\frac{2\times1+3\times -2}{4}=\frac{2-6}{4}=\frac{-4}{4}=1$$
$$x_{2}=\frac{1\times8+3\times 2}{4}=\frac{14}{4}=\frac{7}{2}$$
P = $$\left(-1, \frac{7}{2}\right)$$
$$\frac{AQ}{QB}=\frac{2x}{2x}=1:1$$
$$x_{2}=\frac{1\times2+1\times -2}{2}=0$$
$$y_{2}=\frac{1\times8+1\times 2}{2}=5$$
Q (0, 5)
$$\frac{AR}{RB}=\frac{3x}{x}=3:1$$
$$x_{3}=\frac{1\times2+1\times -2}{4}=1$$
$$y_{3}=\frac{3\times8+1\times 2}{4}=\frac{26}{4}=\frac{13}{2}$$
So, answer is
$$R\left(1, \frac{13}{2}\right)$$
$$P\left(-1, \frac{7}{2}\right)$$
$$Q\left(0, 5\right)$$
Find the area of a rhombus if its vertices are (3, 0), (4, 5), (– 1, 4) and (– 2, – 1) taken in order.
Answer
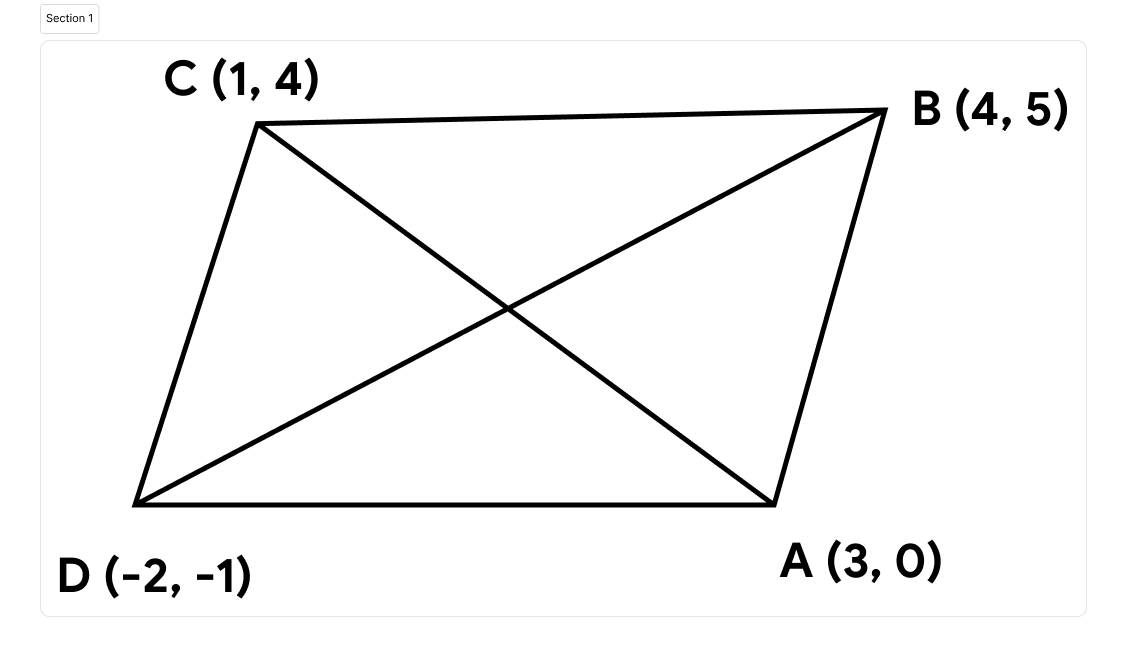
Area of rhombus = $$\frac{1}{2}$$ (product of its diagonals)
So,
AC = $$\sqrt{(3-(-1))^{2}+(0-4)^{2}} = \sqrt{4^{2}+4^{2}} = 4\sqrt{2}$$
BD = $$\sqrt{(4-(-2))^{2}+(5-(-1))^{2}} = \sqrt{6^{2}+6^{2}} = 6\sqrt{2}$$
so, area = $$\frac{1}{2}\times4\sqrt{2}\times6\sqrt{2}$$ = 24 square units
Hope NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.2, helps you in solving problems. If you have any doubts, drop a comment below and we will get back to you.


